DeepLearning

Posted on 2023-10-30 Edited on 2025-02-15 In AI Word count in article: 2.8k Reading time ≈ 10 mins.

Deep learning Notes

#deepLearning/notes

回归问题 (Regression problem)

线性回归 (Linear regression)

神经元输入向量$x=[x_{1},x_{2},…,x_{n}]^T$, 经过函数映射$f_{θ}：x->y$后得到输出y, 其中θ为函数f自身的参数。一种简单的情形是线性变换：$f(x)=w^Tx+b$

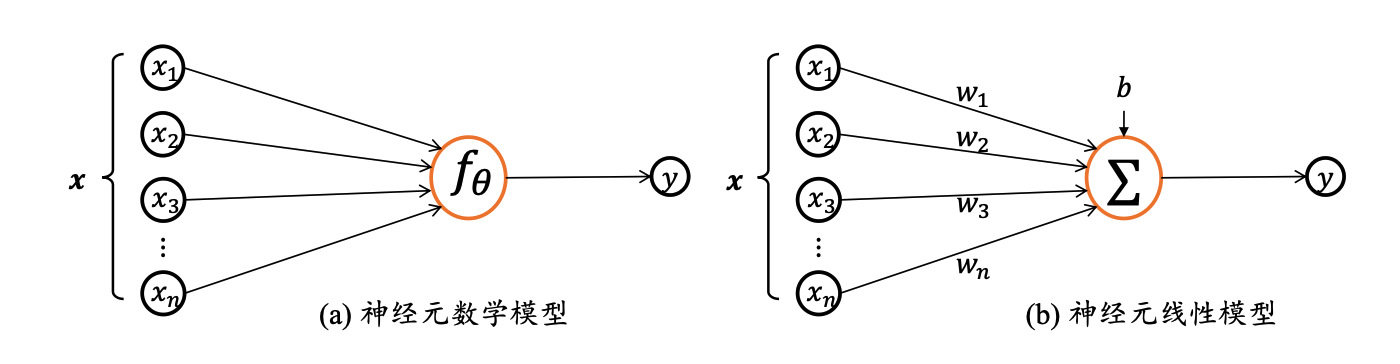
$w$称为权重 (weight)，权重决定了每个特征对我们预测值的影响。 $b$称为偏置(bias)、偏移量 (offset) 或截距 (intercept) 。偏置是指当所有特征都取值为0时，预测值应该为多少。

而在机器学习领域，我们通常使用的是高维数据集，建模时采用线性代数表示法会比较方便。当我们的输入包含$d$个特征时，我们将预测结果$\hat{y}$ （通常使用“尖角”符号表示$y$的估计值）表示为： \[\hat{y} = w_1 x_1 + ... + w_d x_d + b\] 将所有特征放到向量$\mathbf{x} \in \mathbb{R}^d$，并将所有权重放到向量$\mathbf{w} \in \mathbb{R}^d$中，我们可以用点积形式来简洁地表达模型： \[\hat{y} = \mathbf{w}^\top \mathbf{x} + b\]

损失函数 (Loss function)

考虑对于任何采样点，都有可能存在观测误差，我们假设观测误差变量𝜖属于均值为𝜇，方差为$𝜎^2$ 的正态分布(Normal Distribution，或高斯分布，Gaussian Distribution): ${\mathcal{N}}(\mu,\sigma^{2})$，则采样到的样本符合: \[𝑦 = 𝑤𝑥 + 𝑏 + 𝜖, 𝜖~{\mathcal{N}}(\mu,\sigma^{2})\] 一旦引入观测误差后，即使简单如线性模型，如果仅采样两个数据点，可能会带来较大估计偏差。如图 2.4 所示，图中的数据点均带有观测误差，如果基于蓝色矩形块的两个数据点进行估计，则计算出的蓝色虚线与真实橙色直线存在较大偏差。为了减少观测误差引入的估计偏差，可以通过采样多组数据样本集合$𝔻 = \{(x^{(1)},y^{(1)}),\bigl(x^{(2)},y^{(2)}\bigr),\ldots,\bigl(x^{(n)},y^{(n)}\bigr)\}$然后找出一条“最好”的直线，使得它尽可能地让所有采样点到该直线的误差(Error，或损失 Loss)之和最小。

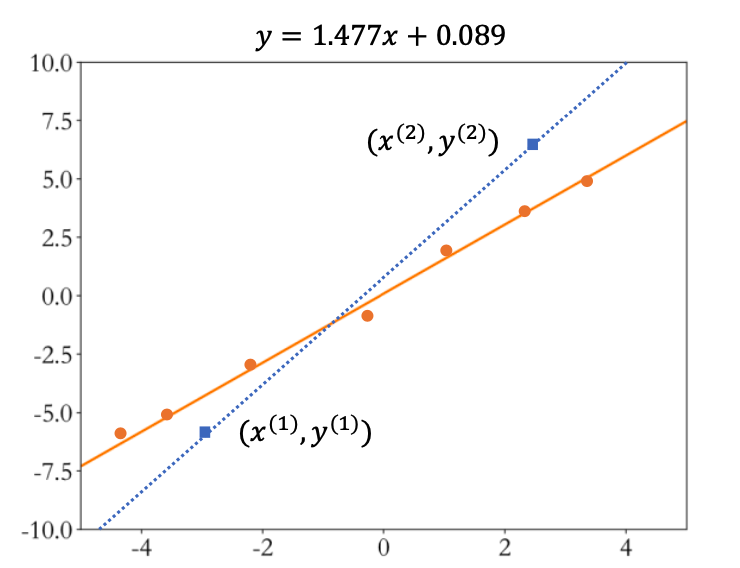
求出当前模型的所有采样点上的预测值$𝑤𝑥^{(𝑖)} + 𝑏$与真实值$𝑦^{(𝑖)}$之间的差的平方和作为总误差$\mathcal{L}$: \[{\mathcal{L}}=\frac{1}{n}\sum_{i=1}^{n}(w x^{(i)}+b-y^{(i)})^{2}\] 然后搜索一组参数$𝑤^∗, 𝑏^∗$使得$\mathcal{L}$最小，对应的直线就是我们要寻找的最优直线: \[w_{i}^*,b^{\ast}=\arg\operatorname*{min}_{w,b}\frac{1}{n}\sum_{i=1}^{n}(w x^{(i)}+b-y^{(i)})^{2}\] 这种误差计算方法称为均方误差(Mean Squared Error，简称 MSE)。

计算损失

# y = wx + b  
def compute_error_for_line_given_points(b, w, points):  
    totalError = 0  
    for i in range(0, len(points)):  
        x = points[i, 0]  
        y = points[i, 1]  
        # computer mean-squared-error  
        totalError += (y - (w * x + b)) ** 2  
    # average loss for each point  
    return totalError / float(len(points))

梯度下降法 (Gradient descent)

我们需要找到一组参数$w^*$和$b^*$，使得ℒ最小。

梯度下降算法（Gradient Descent）是神经网络训练中最常用的优化算法，配合强大的图形处理芯片GPU(Graphics Processing Unit)的并行加速能力，非常适合优化海量数据的神经网络模型，自然也适合优化我们这里的神经元线性模型。

函数的梯度(Gradient)定义为函数对各个自变量的偏导数(Partial Derivative)组成的向量。考虑 3 维函数$𝑧 = 𝑓(𝑥, 𝑦)$，函数对自变量𝑥的偏导数记为${\frac{\partial z}{\partial x}}$, 函数对自变量$𝑦$的偏导数记为${\frac{\partial z}{\partial y}}$，则梯度$∇𝑓$为向量$({\frac{\partial z}{\partial x}},{\frac{\partial z}{\partial y}})$。

函数在各处的梯度方向$∇𝑓$总是指向函数值增大的方向，那么梯度的反方向$−∇𝑓$应指向函数值减少的方向。利用这一性质，我们只需要按照 \[x^{\prime}=x-\eta\cdot\nabla f\] 来迭代更新$x^{\prime}$，就能获得越来越小的函数值，其中𝜂用来缩放梯度向量，一般设置为某较小的值，如 0.01、0.001 等。特别地，对于一维函数，上述向量形式可以退化成标量形式: \[x^{\prime}=x-\eta\cdot{\frac{\mathrm{d}y}{\mathrm{d}x}}\] 通过上式迭代更新$x^{\prime}$若干次，这样得到的$x^{\prime}$处的函数值$y^{\prime}$，总是更有可能比在$𝑥$处的函数值$𝑦$小。通过上式优化参数的方法称为梯度下降算法，它通过循环计算函数的梯度$∇𝑓$并更新待优化参数$𝜃$，从而得到函数$𝑓$获得极小值时参数$𝜃$的最优数值解。

需要优化的模型参数是𝑤和𝑏，因此我们按照下面方式循环更新参数。 \[w^{\prime}=w-\eta{\frac{\partial\mathcal{L}}{\partial w}}\] \[b^{\prime}=b-\eta{\frac{\partial{\mathcal{L}}}{\partial b}}\]

计算梯度

def step_gradient(b_current, w_current, points, learningRate):  
    b_gradient = 0  
    w_gradient = 0  
    N = float(len(points))  
    for i in range(0, len(points)):  
        x = points[i, 0]  
        y = points[i, 1]  
        # grad_b = 2(wx+b-y)  
        b_gradient += (2 / N) * ((w_current * x + b_current) - y)  
        # grad_w = 2(wx+b-y)*x  
        w_gradient += (2 / N) * x * ((w_current * x + b_current) - y)  
    # update w'  
    new_b = b_current - (learningRate * b_gradient)  
    new_w = w_current - (learningRate * w_gradient)  
    return [new_b, new_w]

反向传播 (Backward propagation)

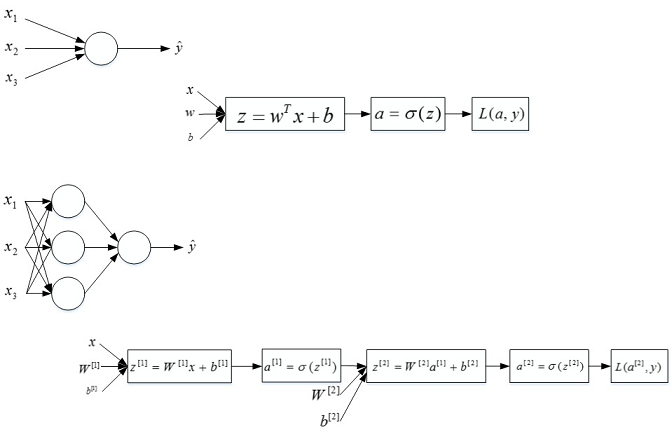
逻辑回归的推导:

\[\left. \begin{matrix} {x} \\ {w} \\ {b} \\ \end{matrix} \right\}\Longrightarrow\mathrm{~}z=w^{T}x+b\implies\alpha=\sigma(z)\mathrm{~}\Longrightarrow L\left(a,y\right)\] 正向传播步骤:计算$z^{[1]}, a^{[1]}$，然后$z^{[2]},a^{[2]}$，然后损失函数$L$

$$_{d{w}=d{z} x,d{b}=d{z}}

_{d{z}=d{a}g^{'}(z),g(z)!=!(z)!, !=!,,,g!(z)!=!g^{'}(z)}

\underbrace{\alpha=\sigma(z)\mathrm{~}\Longrightarrow L\left(a,y\right)}_{d a={\frac{d}{d a}}\,L{\big(}a,y{\big)}=\left(-y\log\alpha-{\big(}1-y{\big)}\log{\big(}1-a{\big)}\right)^{\prime}=-\,{\frac{y}{a}}+{\frac{1-y}{1-a}}}$$

前向传播：计算$z^{[1]}$, $a^{[1]}$, 再计算$z^{[2]}$, $a^{[2]}$，，最后得到loss function。

反向传播： \[dz^{[2]}=a^{[2]}-Y\] \[dW^{[2]}=\frac{1}{m}dz^{[2]}a^{[1]T}\] \[{\cal L}\,=\,\frac{1}{m}\sum_{i}^{n}\,L(\hat{y},y)\] \[db^{\left[2\right]}=\frac{1}{m}np.sum(dZ^{\left[2\right]},axis=1,keepdims=True)\] \[d Z^{[1]}=W^{[2]T}d Z^{[2]}*g^{[1]\prime}(Z^{[1]})\] \[d W^{[1]}=\frac{1}{m}d Z^{[1]}X^{T}\] \[db^{\left[1\right]}=\frac{1}{m}np.sum(dZ^{\left[1\right]},axis=1,keepdims=True)\]

# Backward propagation: calculate dW1, db1, dW2, db2. 
### START CODE HERE ### (≈ 6 lines of code, corresponding to 6 equations on slide above)
dZ2 = A2 - Y
dW2 = np.dot(dZ2, A1.T) / m
db2 = np.sum(dZ2, axis = 1, keepdims = True) / m
dZ1 = np.multiply(np.dot(W2.T,dZ2), 1 - np.power(A1, 2))
dW1 = np.dot(dZ1, X.T) / m
db1 = np.sum(dZ1, axis = 1, keepdims = True) / m

# 浅层神经网络(Shallow neural networks)

神经网络概述（Neural Network Overview）

## 神经网络的表示（Neural Network Representation ）

单隐藏层神经网络就是典型的浅层（shallow）神经网络 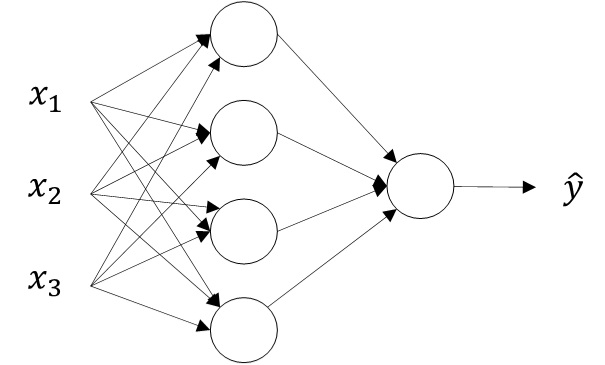单隐藏层神经网络也被称为两层神经网络（2 layer NN)

第$l$层的权重$W^{[l]}$叫维度的行等于$l$层神经元的个数，列等于$l-1$层神经元的个数; 第$i$层常数项维度的行等于$I$层神经元的个数，列始终为1 ## 计算一个神经网络的输出（Computing a Neural Network's output ）

两层神经网络可以看成是逻辑回归再重复计算一次

逻辑回归的正向计算可以分解成计算$z$和$a$的两部分:

\[z=w^{T}x+b\]

\[ a=\sigma(z)\]

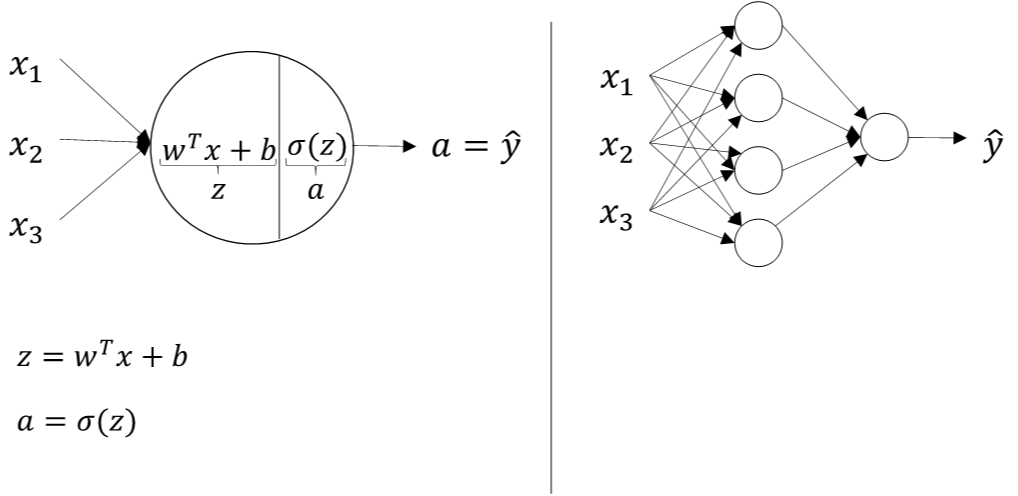
两层神经网络，从输入层到隐藏层对应一次逻辑回归运算；从隐藏层到输出层对应一次逻辑回归运算 \[z^{[1]}=W^{[1]}x+b^{[1]}\]

\[a^{[1]}\ =\sigma(z^{[1]})\] \[z^{[2]}=W^{[2]}a^{[1]}+b^{[2]}\] \[a^{[2]}\ =\sigma(z^{[2]})\]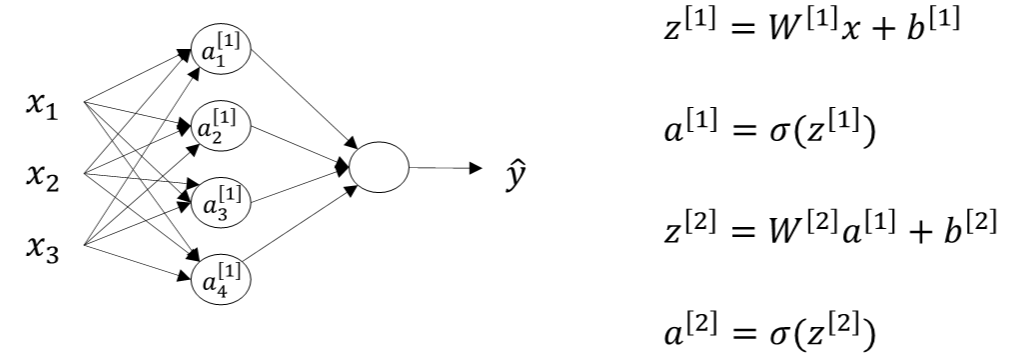

多样本向量化（Vectorizing across multiple examples ）

矩阵运算的形式： \[{Z}^{[1]}=W^{[1]}{X}+b^{[1]}\] \[A^{(1)}=\sigma(Z^{(1)})\] \[Z^{(2)}=W^{[2]}A^{[1]}+b^{[2]}\] \[A^{(2)}=\sigma(Z^{(2)})\] 行表示神经元个数，列表示样本数目 m

激活函数（Activation functions）

sigmoid函数 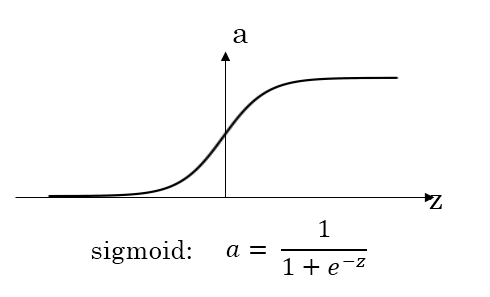sigmoid

tanh函数 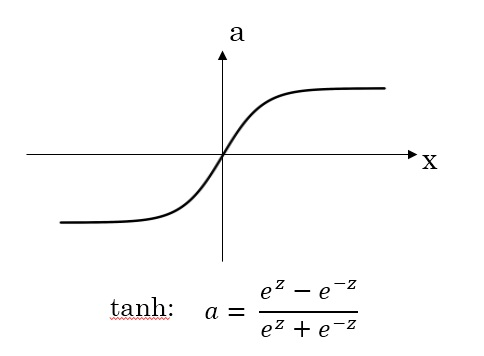tanh

ReLU函数

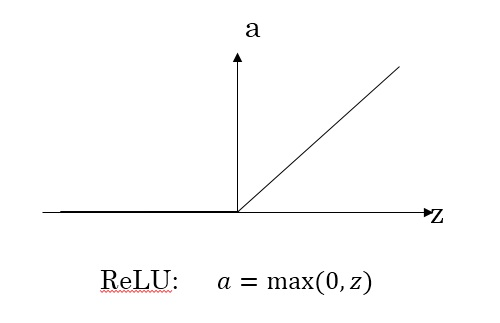
Leaky ReLU函数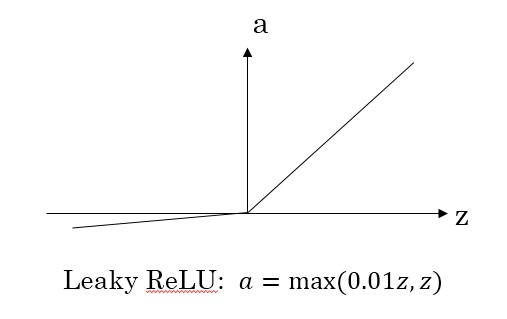

对于隐藏层的激活函数，$tanh$函数要比$sigmoid$函数表现更好一些。因为$tanh$函数的取值范围在$[-1,+1]$之间，隐藏层的输出被限定在$[-1,+1]$之间，可以看成是在0值附近分布，均值为0。这样从隐藏层到输出层，数据起到了归一化(均值为0)的效果。

对于输出层的激活函数，因为二分类问题的输出取值为${0,+1}$，所以一般会选择$sigmoid$作为激活函数选择$ReLU$作为激活函数能够保证$x$大于零时梯度始终为1，从而提高神经网络梯度下降算法运算速度。但当$z$小于零时，存在梯度为0的缺点

$Leaky ReLU$激活函数，能够保证$z$小于零时梯度不为0

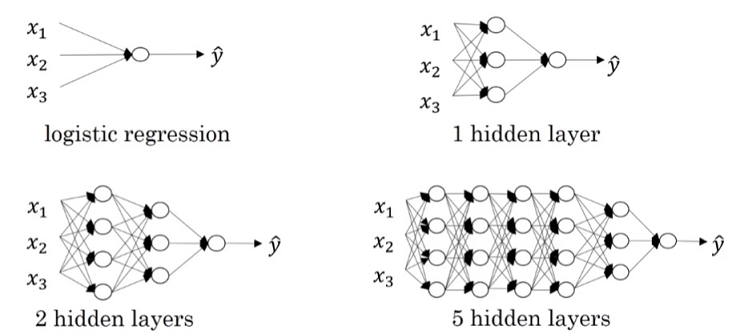
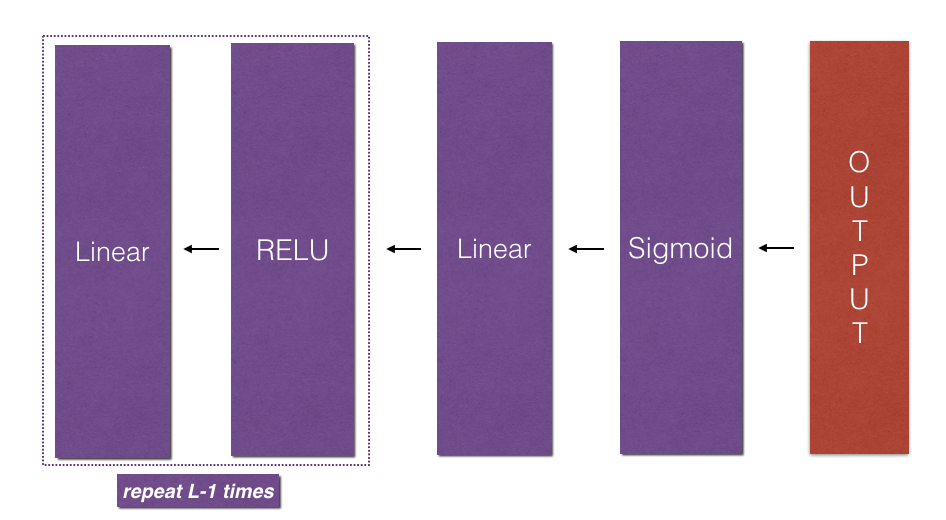
深层神经网络(Deep Neural Networks)

深层神经网络（Deep L-layer neural network）

$L−layer NN$，则包含了$L−1$个隐藏层，最后的$L$层是输出层 $a^{[l]}$和$W^{[l]}$中的上标$l$都是从$1$开始的，$l=1,⋯,L$ 输$x$记为$a^{[0]}$, 把输出层${\hat{y}}$记为$a^{[L]}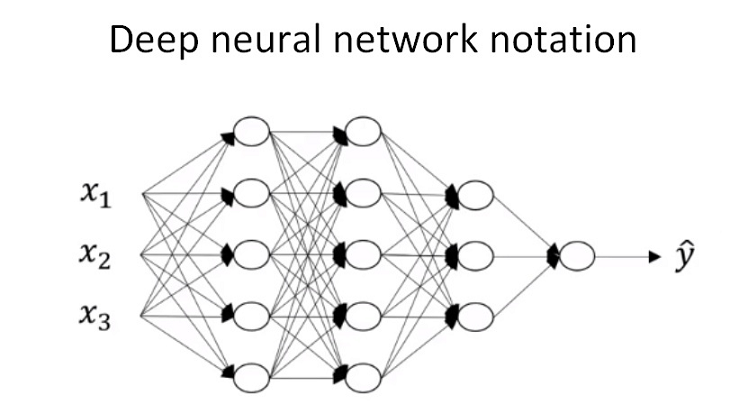$ ## 前向传播和反向传播（Forward and backward propagation）

正向传播过程

\[z^{[l]}=W^{[l]}a^{[l-1]}+b^{[l]}\] \[a^{[l]}=g^{[l]}(z^{[l]})\] m个训练样本，向量化形式为: \[Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}\] \[A^{[l]}=g^{[l]}(z^{[l]})\] ### 反向传播过程 \[d z^{[l]}=d a^{[l]}*g^{[l]^{'}}(z^{[l]})\] \[d W^{[l]}=d z^{[l]}\cdot a^{[l-1]^{T}}\] \[d b^{[l]}=d z^{[l]}\] \[d a^{[l-1]}=W^{[l]T}\cdot d z^{[l]}\] 得到： \[d z^{[l]}=W^{[l+1]T}\cdot d z^{[l+1]}\ast g^{[l]'}(z^{[l]})\]m个训练样本，向量化形式为: \[d Z^{[l]}=d A^{[l]}*g^{[l]^{\prime}}(Z^{[l]})\] \[d W^{[l]}=\frac{1}{m}d Z^{[l]}\cdot A^{[l-1]T}\] \[d b^{[l]}=\frac{1}{m}n p.s u m(d Z^{[l]},a x i s=1,k e e p d i m=T r u e)\] \[d A^{\left[l-1\right]}=W^{\left[l\right]T}\cdot d Z^{\left[l\right]}\] \[d Z^{[l]}=W^{[l+1]T}\cdot d Z^{[l+1]}\ast g^{[l]^{\prime}}(Z^{[l]})\] ## 层网络中的前向传播（Forward propagation in a Deep Network ）

对于第$l$层，其正向传播过程的$Z^{[l]}$和$A^{[l]}$可以表示为： \[Z^{[l]}=W^{[l]}A^{[l-1]}+b^{[l]}\] \[A^{[l]}=g^{[l]}(Z^{[l]})\] 其中$l=1,\cdots,L$

搭建神经网络块（Building blocks of deep neural networks）

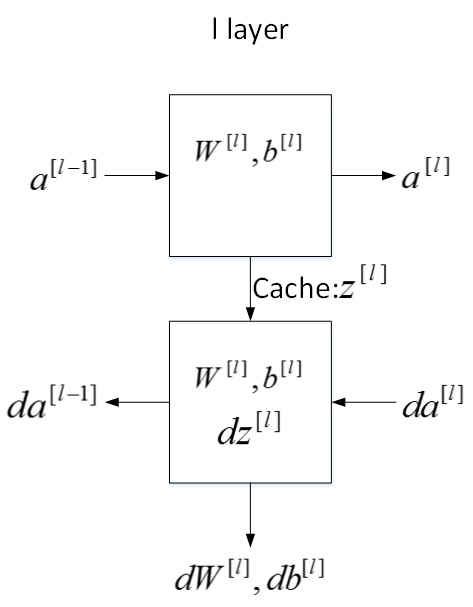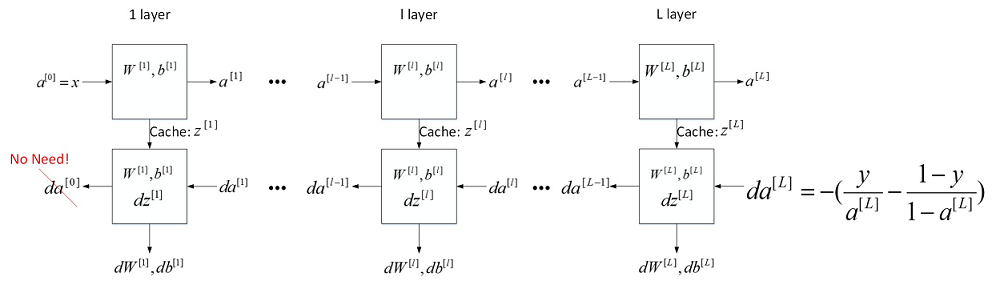
第$l$层的流程块图对于神经网络所有层，整体的流程块图正向传播过程和反向传播过程如下所示： ## 参数 VS 超参数（Parameters vs Hyperparameters）

神经网络中的参数是$W^{[l]}$和$b^{[l]}$ 超参数则是例如学习速率$\alpha$，训练迭代次数$N$，神经网络层数$L$，各层神经元个数$n^{[l]}$，激活函数$g(z)$等叫做超参数的原因是它们决定了参数$W^{[l]}$和$b^{[l]}$的值

如何设置最优的超参数： 通常的做法是选择超参数一定范围内的值，分别代入神经网络进行训练，测试cost function随着迭代次数增加的变化，根据结果选择cost function最小时对应的超参数值